1 Introduction:
In this project we tried to develop a 4X4 tic-tac-toe game. Our first target was to
make a multiplier game where the microcontroller’s job was to provide an environment for
the gameplay of two players and display who has won. We achieved that. After achieving
this, our goal was to make a single-player game where a human will play against an AI. This
AI will be programmed in the microcontroller. But in course of this we realised that in case of
a 4X4 tic-tac-toe game, for an unbeatable AI to work, it needs to check almost 15! number of
combination in the initial stages of the game which was a huge task and was not possible to
achieve in a microcontroller. So instead we downgraded our goal to make a 3X3 single-player
tic-tac-toe.
2 Hardware configurations:
LCD:
Libraries used:
grlib – this library contains all the functions to draw on the LCD.
touch – this library contains all the functions related to touchscreen.
Note that these libraries are available on the latest Tiva library so please download the latest
one from TI website.
Widget for touch screen:
The Push Button widget provides a method to take input from the user through the
touchscreen LCD. There is a function that gets executed whenever an user touches that
portion of screen where the pushbutton is defined. A programmer can write that function.
Touch sense:
WidgetMessageQueueAdd()- this function add the message from the widget in a
queue and executes the corresponding functions sequentially.
Edit the tm4c123gh6pm_startup_ccs_gcc.c file:
a. Add this function TouchScreenIntHandler in ADC Sequence 3 interrupt.
Handles the ADC interrupt for the touch screen.
This function is called when the ADC sequence that samples the touch screen has
completed its acquisition. The touch screen state machine is advanced and the acquired
ADC sample is processed appropriately.
b. Increase the stack size to static uint32_t pui32Stack[4096]. As the code contains a lot of
function calling , It requires a stack of size more than 512 Bytes(default).
3 Algorithm and code structure:
Min max algorithm:
Minimax is a kind of backtracking algorithm that is used in decision making and
game theory to find the optimal move for a player, assuming that your opponent also plays
optimally. It is widely used in two player turn-based games.
In Minimax the two players are called maximizer and minimizer. The maximizer tries
to get the highest score possible while the minimizer tries to do the opposite and get thelowest score possible (that is most optimal for the opponent). This strategy is a corollary of
Nash Equilibrium state.
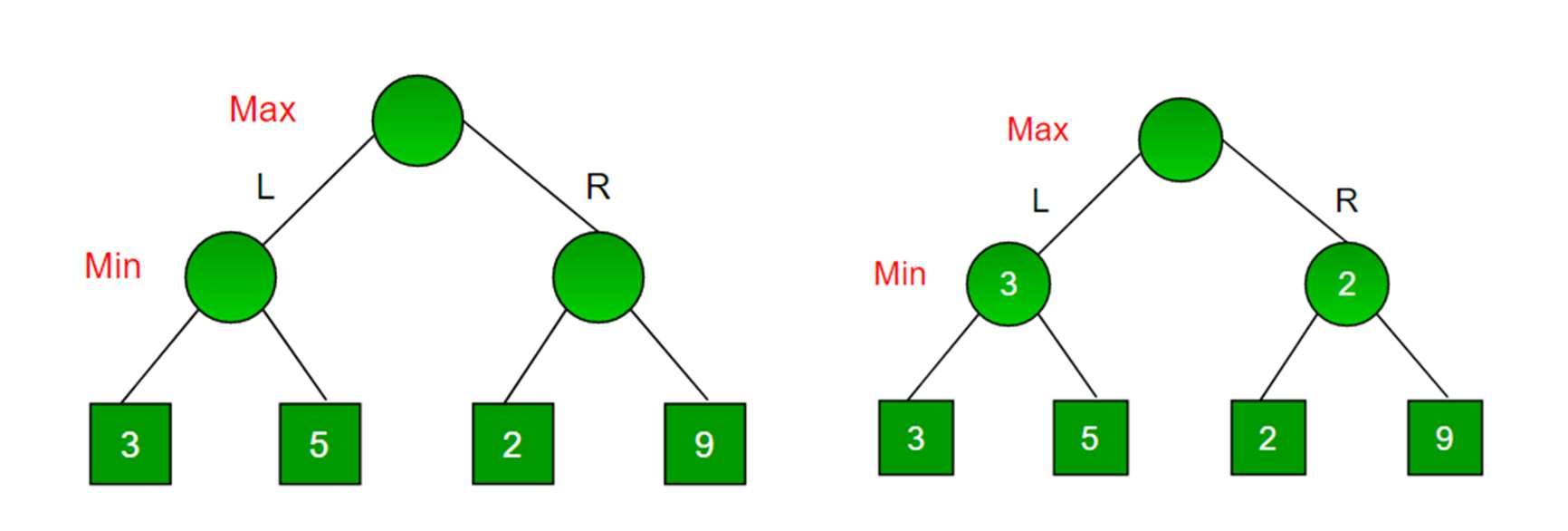
The above figure demonstrates a game where the computer (root node) is at a state
where it has two moves available. Depending on computer’s move the opponent also makes a
move. The opponent also has two moves available , either go left or right. We note that the
leaf note is a determining node i.e. game ends there and depending upon who wins, a score is
assigned. As the scores are calculated with respect to the computer, the more the score merrier
for the computer. But here we assume the opponent also plays optimally. So that is why the
computer when it’s turn will try to maximize the scores whereas the opponent will try to
minimize the scores. As an example, let’s say at the root node the computer plays Left , Now
the opponent has two options either go Left or right but taking the right option is not
beneficial for the opponent as the score is higher. So if we assume the opponent plays
optimally , it will play the left move , which will return 3 to that node. Similarly in case of
right move of computer the opponent will play left move, which will return value of 2. Now
computer will take maximum of them i.e. 3 . So the optimal move for computer is to go left.
Connection with Nash equilibrium:
Even though there is a value of 9 on the right subtree, the minimizer will never pick
that. We must always assume that our opponent plays optimally.
This is Nash Equilibrium . Even though opponent does not play optimally we will
only gain never lose points.
Min max algo for tic-tac-toe:-
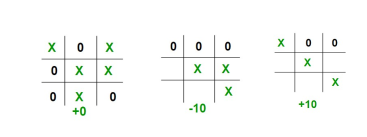
fig:Scores at the base case
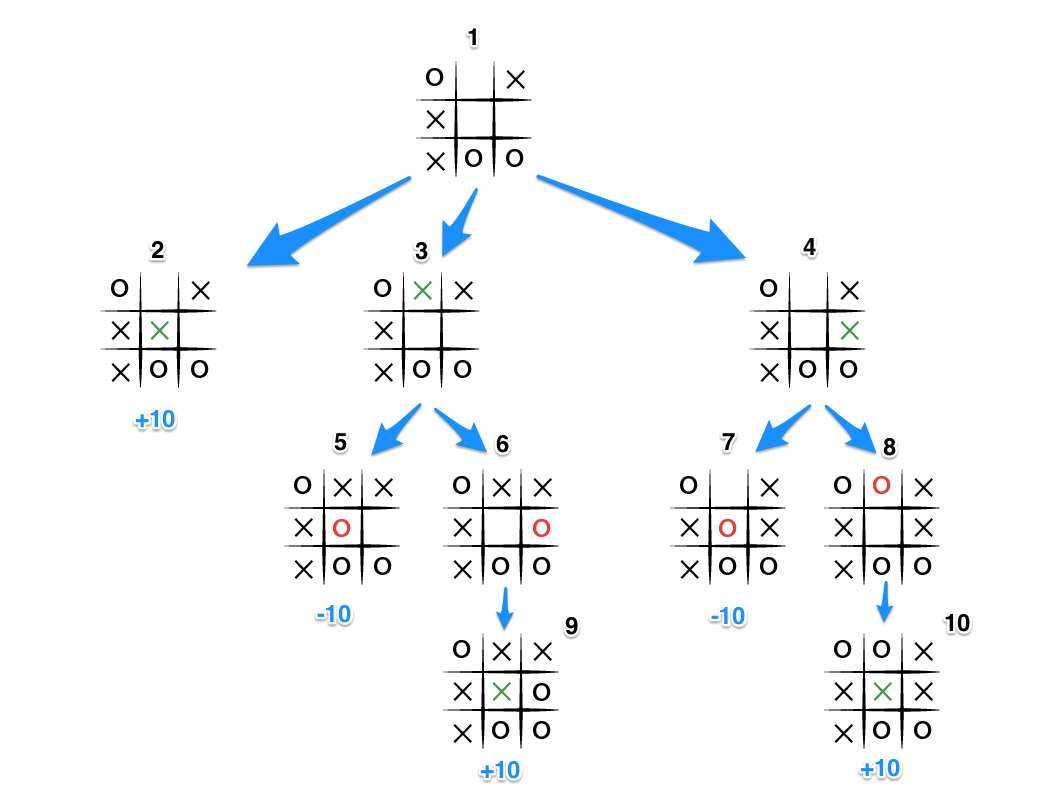
Here we are considering a state of the move close to the end of the game and it is the
computer’s turn. We see that the computer can go to 3 states i.e. 2 , 3 ,4 . Now it is the
opponent’s turn it will try to take the minimum. Then it is again the computer’s turn until
someone wins. So between 5 and 6 it will chose 5. Similarly between 7 and 8 it will choose 7.
So max score for the computer is at the 2nd state +10. So it will take that path. Note that in
reality the opponent may not always play the optimal move but it will only increase the
chances of winning of the AI.
Make AI smarter (Depth Penalization):
Move A : X can win in 2 move
Move B : X can win in 4 moves
Our evaluation function will return a value of +10 for both moves A and B. Even
though the move A is better because it ensures a faster victory, our AI may choose B
sometimes. To overcome this problem we subtract the depth value from the evaluated
score. This means that in case of a victory it will choose a the victory which takes least
number of moves and in case of a loss it will try to prolong the game and play as many
moves as possible.
Minmax pseudo code:-
function findBestMove(board):
bestMove = NULL
for each move in board :
if current move is better than bestMove
bestMove = current move
return bestMove
function minimax(board, depth, isMaximizingPlayer):
if current board state is a terminal state :
return value of the boardif isMaximizingPlayer :
bestVal = -INFINITY
for each move in board :
value = minimax(board, depth+1, false)
bestVal = max( bestVal, value)
return bestVal
else :
bestVal = +INFINITY
for each move in board :
value = minimax(board, depth+1, true)
bestVal = min( bestVal, value)
return bestVal
Code structure:-
int main()
{
Print Welcome screen();
While(1)
{
Wait for user input
Go to single player or multi player
}
}
single or multi player()
{
Print grid();
While(1)
{
Wait for user input
Give comp output if single player via minmax algo
Check if anybody has won then go to winner display screen
}
}
winner()
{
Print who is Winner screen;
While(1)
{
Wait for user input
On touching winner break and go back to welcome screen
}
}
minmax(current board state , IsMax)
{
If someone has won
Return score -10 or 10
Else
Return (max(Minmax(depth +1))) in case of maximizer
Return (min(Minmax(depth +1))) in case of maximizer
}
FindBestMove(current board state)
{
Check for all possible options in the board and return location of
max(minmax())
}
4 Future Work:
In future 4X4 tic-tac-toe can be implemented for a microcontroller. This can be done
by generating a dataset with FindingBestMove function and training a Deep Neural Network
with this. After that the generated weights can be fed to microcontroller and microcontroller
can generate the output just by computing the output of the DNN. This will be much more
computationally inexpensive than the minmax algorithm.
5 Demo video Link: https://youtu.be/4LSHJbIIaIs
6 References:
1. https://www.geeksforgeeks.org/minimax-algorithm-in-game-theory-set-3-tic-tac-toe-ai-
finding-optimal-move/
2. https://www.neverstopbuilding.com/blog/minimax
Recent Comments