Motivation:
In the context of sensor network (e.g., smart grid, Home Area Network (HAN), etc.), each network node (for HAN, each HAN) periodically sends data to base station (for HAN, sends the electricity consumption to the home to the local utility). According to the coming data the base station might process the aggregate of incoming data to get some information about underlying processes (for HAN, computing electric bill and utilize this aggregated information in forecasting the future power demand and electric price for a certain region).
Solution:
Various nodes can encrypt the data using public key, one node (for HAN, smart meter aggregates the appliances’ readings) will aggregate and forward to base station which decrypts the sum using secret key. Note that, here as this is public key encryption, so any node can encrypt but only base station can decrypt.
We tried to implement this data aggregation scheme using lattice-based additively homomorphic encryption which can encrypt and aggregate
entire vector/ arrays together and is also quantum- secure, but there were memory issues with that. So we are implementing the same
using Elliptic Curve based homomorphic encryption.
Elliptic Curve Cryptography
The mathematical operations of ECC is defined over the elliptic curve y2 = x3 + ax + b, where 4a3 + 27b2 ≠ 0. Each value of the ‘a’ and ‘b’ gives a different elliptic curve. One main advantage of ECC is its small key size. A 160-bit key in ECC is considered to be as secured as 1024-bit key in RSA.
Discrete Logarithm Problem: The security of ECC depends on the difficulty of Elliptic Curve Discrete Logarithm Problem. Let P and Q be two points on an elliptic curve such that kP = Q, where k is a scalar. Given P and Q, it is computationally infeasible to obtain k, if k is sufficiently large. k is the discrete logarithm of Q to the base P.
Hence the main operation involved in ECC is point multiplication. i.e. multiplication of a scalar k with any point P on the curve to obtain another point Q on the curve.
Preliminaries:
Point multiplication
In point multiplication a point P on the elliptic curve is multiplied with a scalar k using elliptic curve equation to obtain another point Q on the same elliptic curve. i.e. kP=Q .
Point multiplication is achieved by two basic elliptic curve operations
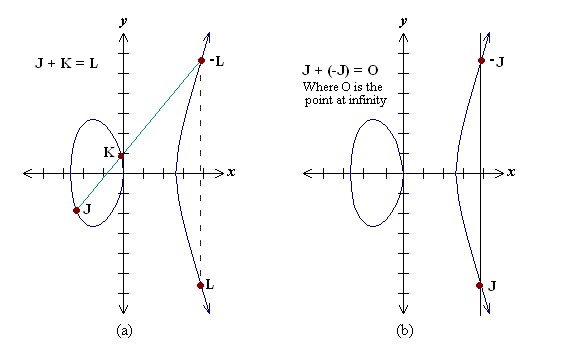
• Point addition, adding two points J and K to obtain another point L i.e., L = J + K.
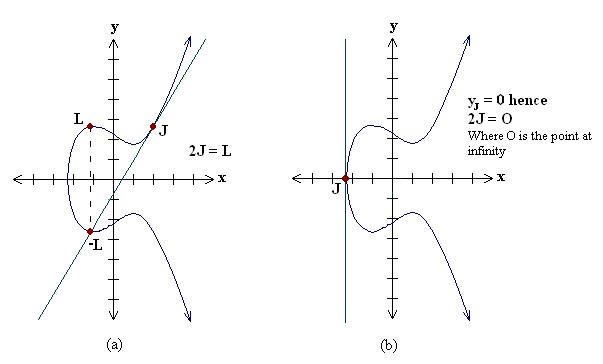
• Point doubling, adding a point J to itself to obtain another point L i.e. L = 2J.
Here is a simple example of how point multiplication is achieved. If k = 23 then kP = 23.P = 2(2(2(2P) + P) + P) + P.
Thus point multiplication uses point addition and point doubling repeatedly to find the result. The above method is called ‘double and add’ method for point multiplication.
Point addition:
Point addition is the addition of two points J and K
on an elliptic curve to obtain another point L on the
same elliptic curve.
Consider two points J and K on an elliptic curve as
shown in figure (a). If K ≠ -J then a line drawn through the
points J and K will intersect the elliptic curve at exactly one more point –L. The reflection of the point –L with respect to x-axis gives the point L, which is the result of addition of points J and K.
Thus on an elliptic curve L = J + K.
If K = -J the line through this point intersect at a point at infinity O. Hence J + (-J) = O.
This is shown in figure (b). O is the additive identity of the elliptic curve group.
A negative of a point is the reflection of that point with respect to x-axis.
Point doubling:
Point doubling is the addition of a point J on the elliptic curve
to itself to obtain another point L on the same elliptic curve
To double a point J to get L, i.e. to find L = 2J, consider a point J
on an elliptic curve as shown in figure (a). If y coordinate of the
point J is not zero then the tangent line at J will intersect the elliptic curve at exactly one more point –L.
The reflection of the point –L with respect to x-axis gives the point L, which is the result of doubling the point J. Thus L = 2J.
If y coordinate of the point J is zero then the tangent at this point intersects at a point at infinity O.
EC on Prime Field
The elliptic curve operations defined above are on real numbers. Operations over the real numbers are slow and inaccurate due to round-off error. Cryptographic operations need to be faster and accurate. To make operations on elliptic curve accurate and more efficient, the curve cryptography is defined over finite fields.
The equation of the elliptic curve on a prime field Fp is y2 mod p= x3 + ax + b mod p, where 4a3 + 27b2 mod p ≠ 0. Here the elements of the finite field are integers between 0 and p-1
In our case we are operating in 256 bit prime field, so the point coordinates are 256 bits each and scalar also uses 256 bits.
Also the curve we are using is the NIST P-256 curve which is standard at 128-bit security level.
Analytical Expressions in Prime Field:
Point Addition :
Consider two distinct points J and K such that J = (xJ, yJ) and K = (xK, yK)
Let L = J + K where L = (xL, yL), then xL = s2 + s + xJ + xK + a, yL = s (xJ + xL) + xL + yJ , s = (yJ + yK)/(xJ + xK), s is the slope of the line through J and K.
If K = -J i.e. K = (xJ, xJ + yJ) then J + K = O. where O is the point at infinity.
If K = J then J + K = 2J then point doubling equations are used. Also J + K = K + J
Point Subtraction :
Consider two distinct points J and K such that J = (xJ, yJ) and K = (xK, yK)
Then J – K = J + (-K) where -K = (xk, xk + yk)
Point Doubling:
Consider a point J such that J = (xJ, yJ), where xJ ≠ 0 Let L = 2J where L = (xL, yL), Then
xL = s2 + s + a, yL = xJ2 + (s + 1)*xL , s = xJ + yJ/ xJ, s is the tangent at point J and a is one of the parameters chosen with the elliptic curve
If xJ = 0 then 2J = O, where O is the point at infinity.
Implementation Details:
Using this ECC based encryption we will perform data aggregation, i.e., Enc(m1)+Enc(m2)=Enc(m1+m2) followed by the idea of homomorphism.
We are using NIST P-256 curve which is standard at 128 bit security level.
The point co-ordinates are 256 bit each and scalars are also 256 bits. So, to have a 256 bit long integer we are implementing this by a structure
struct ecclib_mpi
{
uint32_t p[8]; // limbs
};
And the affine co-ordinates are realized as follows:
// Elliptic Curve Point
struct ecclib_ecp
{
struct ecclib_mpi X; // x-coordinate
struct ecclib_mpi Y; // y-coordinate
uint32_t inf; // flag for point at infinity
};
The main operation of ECC, i.e., point multiplication is done by the following function:
// Q = k(P)
int ecclib_ecp_affine_scalar_mul( struct ecclib_ecp *Q, struct ecclib_ecp *P, struct ecclib_mpi *k,
struct ecclib_mpi *param_a, struct ecclib_mpi *param_b,
struct ecclib_mpi *order, struct ecclib_mpi *prime );
The point addition is done by,
// P3 = P1 + P2
void ecclib_ecp_affine_add( struct ecclib_ecp *P3, struct ecclib_ecp *P1, struct ecclib_ecp *P2,
struct ecclib_mpi *param_a, struct ecclib_mpi *prime );
And the point doubling is done by,
// P3 = 2(P1)
void ecclib_ecp_affine_dbl( struct ecclib_ecp *P3, struct ecclib_ecp *P1,
struct ecclib_mpi *param_a, struct ecclib_mpi *prime );
All of the above mentioned functions are implemented using the analytical expression for prime field explained earlier.
Addition/ Subtraction of each 256 bit integer is done by adding/ subtracting 8 32-bit integer one by one and propagating the carry/borrow of each stage to the next stage.
All the stages (i.e., key generation, encryption, decryption, data aggregation) are timed by hardware timer to get an idea about the total latency. Also for printing the important variables (i.e. message ,ciphertext, public key, etc.) after each stage a self-made Uart module is used.
Result:
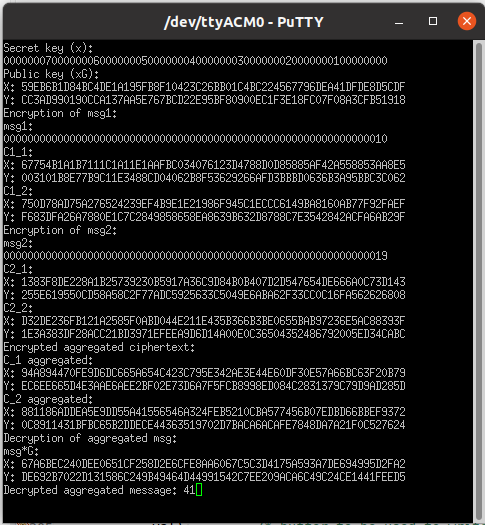
The whole operation of data aggregation, i.e., from key generation to aggregated data encryption can be seen in the PuTTY window.
The public key (xG) is available to every sensor node.
Using this public key one sensor node encrypts the message (msg1=16) and generates ciphertext (C1_1,C1_2)
And another sensor node encrypts another message (msg2=25) and generates ciphertext (C2_1, C2_2)
Now at data aggregation step we add these two ciphertexts using point addition in encrypted domain and we get (C_1, C_2).
The encrypted aggregated ciphertext now can be decrypted by the base-station as follows
(C_2 – x*C_1 =mG), where x= secret key (base- station
knows the secret key so decryption can be done)
From this mG we perform a small searching (as m is small) and find the corresponding aggregated message=
msg1 (16)+msg2 (25)= 41
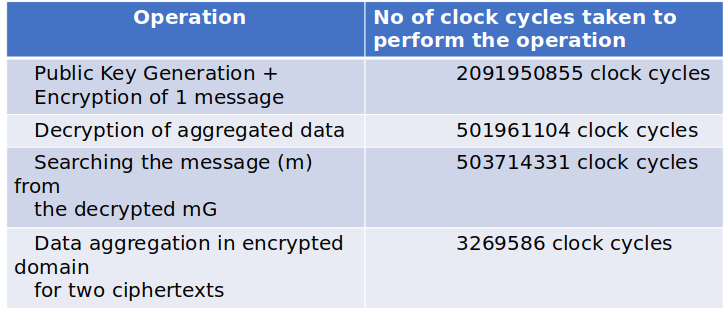
These clock cycles are measured using hardware timer and incrementing a variable (time_cycle_count ) inside an interrupt routine after each completion of total count (i.e., 65536).
Note: These number of clock cycle measured values are not affected by printing command through UART in the code in between different intermediate steps, as in between timer count we are not printing any values.
Remarks:
Note that this scheme can be extended more data aggregation of more messages as well
The searching scheme of message at decryption stage can be made more optimized using better algorithm – “Baby step giant step” which is O(sqrt(n)) instead of O(n), where n is the maximum value of message (in our case n=63). But it requires creating a precomputation table and while implementing that we might run into memory issues.
Even if we do some of the noted optimizations possible as of now (e.g., searching, etc.) in the existing code, then also the elliptic curve execution might run terribly slow in software, which is the motivation for hardware acceleration for these kind of cryptographic schemes.
Demo: Computation framework for lattice based homomorphic encryption
Code:Project Workspace
Recent Comments