Data Encryption using AES Algorithm in TIVA Board
Introduction:
As application such as Internet of Things are increasing day by day, need of having secured communication/data transmission between embedded systems are a must
requirement. Microcontrollers are the key component of most of the embedded systems and systems are build around these devices. Few higher end
microcontrollers come with dedicated inbuilt hardware for the data encryption and decryption and thus provide the data security feature. But all applications may not
call for these types of dedicated microcontrollers due to the cost and minimal requirements. Low-cost microcontrollers such as TM4C123GH6PM even though
are having interfaces such as SPI, I2C, CAN, UART etc, does not come with dedicated hardware for data encryption and decryption. These types of
microcontrollers need to implement the data encryption decryption in software considering the resource constraints like Time, Memory etc.
Advanced Encryption Standard (AES) is a widely used encryption standard, based on design principle known as substitution permutation network, which considered
to be highly secure electronic data transfer. As we discussed before, few microcontrollers come with AES support in hardware itself. In this project we are
implementing AES standard for encryption and decryption as C library which can be used for small embedded applications. Implemented library is demonstrated using
a UART based console program using TM4C123GH6PM Tiva board. Details of steps included in the AES Encryption and Decryption are explained briefly
in the coming section along with specific implementation details.
AES Encryption Decryption
AES is a subset of the Rijndael block cipher developed by two Belgiancryptographers, Vincent Rijmen and Joan Daemen, who submitted a proposal to
NIST during the AES selection process. It was the winner of this competition and thus named “AES”, for advanced encryption Standard by 2001. It is now the most
widely used symmetric key encryption in the world.
Terminology
There are terms that are frequently used throughout this report that need to be clarified.
Block: AES is a block cipher. This means that the number of bytes that it encrypts is fixed. AES can currently encrypt blocks of 16 bytes at a time; no other block
sizes are presently a part of the AES standard. If the bytes being encrypted are larger than the specified block, then AES is executed concurrently. This also means
that AES must encrypt a minimum of 16 bytes. If the plain text is smaller than 16 bytes, then it must be padded. Simply said the block is a reference to the bytes that
are processed by the algorithm.
State: Defines the current condition (state) of the block. That is the block of bytes that are currently being worked on. The state starts off being equal to the block,
however it changes as each round of the algorithms executes. Plainly said this is the block in progress.
AES Encryption:
The Advanced Encryption Standard (AES) is an algorithm used to encrypt and decrypt data to protect the data when it is transmitted electronically. The algorithm
described by AES is a symmetric-key algorithm, meaning the same key is used for both encrypting and decrypting the data.
The AES algorithm allows for the use of cipher keys that are 128, 192, or 256 bits (16, 24 or 32 byte) long to protect data in 16-byte blocks. The main reason behind
the security offered by the AES is due to its bigger key length itself which makes the no of keys to be checked very huge for brute force attacks.
AES is an iterated block encryption mechanism, which means same operations are repeated many times on a particular message block. One iteration of this operations
is called a round. All round except final round are similar and specific bytes derived from initially provided key is used in each round. The process by which theseextended keys generating from initially provided key is called key expansion.
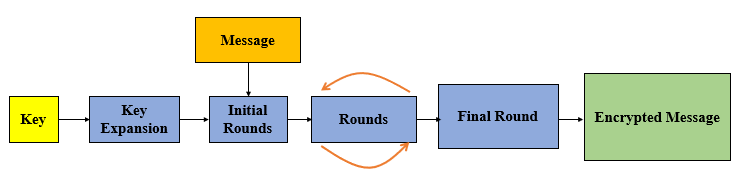
Figure 1: AES encryption flow diagram
The number of rounds the operations are repeated depends up on the key length. Below table gives the details of the no of round and length of expanded key including
the initial key specified by the standard for each of the key lengths.

A specific round contains the following operations or steps.
1) Sub Byte Step
2) Shift Row or Rotation
3) Mix Column
4) Add Round Key
Every round except last round is having all these steps while last round is not having
Mix column step included in that.
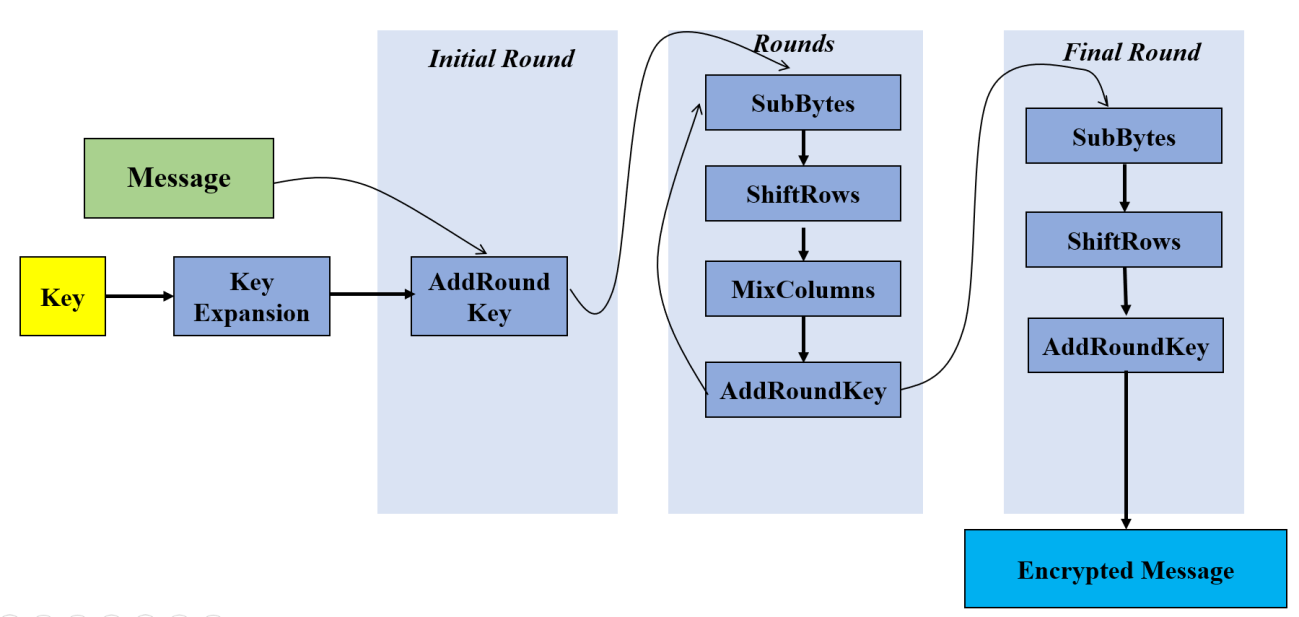
Figure 2 Detailed block diagram of AES encryption.
Detailed block diagram of AES encryption with steps included in each round is given in Figure 2.
Steps included in each step is explained some detail in coming sections.
Key Expansion
Key expansion is the routine or the process by which the initial key is expanded and
keys for each round is calculated. This is done by following few fixed steps.
In case of 16-byte key, AES key expansion algorithm takes as input a four-word (16- byte) key and produces a linear array of 44 words (176 bytes). This is sufficient to
provide a four-word round key for the initial AddRoundKey stage and each of the
10 rounds of the cipher. Similar operation only done in case of 24 and 32 byte key lengths also.
Let’s say that we have the four words of the round key for the i th round:
w[i] ,w[i+1], w[i+2], w[i+3]
For these to serve as the round key for the i th round, i must be a multiple of 4. These will obviously serve as the round key for the (i/4)th round.
For example, w[4], w[5], w[6], w[7] is the round key for round 1, the sequence of words w[8], w[9], w[10], w[11] the round key for round 2, and so on.
Now we need to determine the words:
w[i+4],w[i+5], w[i+6], w[i+7] from the words w[i], w[i+1], w[i+2], w[i+3]
w[i+5] = w[i+4] xor w[i+1]
w[i+6] = w[i+5] xor w[i+2]
w[i+7] = w[i+6] xor w[i+3]
w[i+4] is the beginning word of each 4-word grouping in the key expansion. The beginning word of each round key is obtained by:
w[i+4] = w[i] xor g(w[i+3])
That is, the first word of the new 4-word grouping is to be obtained by XOR’ing the first word of the last grouping with what is returned by applying a function g() to the
last word of the previous 4-word grouping. The key is copied into the first four words of the expanded key. The remainder of
the expanded key is filled in four words at a time. Each added word w[i] depends on the immediately preceding word, w[i – 1], and the word four positions back, w[i -4].
In three out of four cases, a simple XOR is used. For a word whose position in thew array is a multiple of 4, a more complex function is used. The following figureillustrates the generation of the expanded key, using the symbol g to represent that complex function. The function g consists of the following steps:
illustrates the generation of the expanded key, using the symbol g to represent that complex function. The function g consists of the following steps:
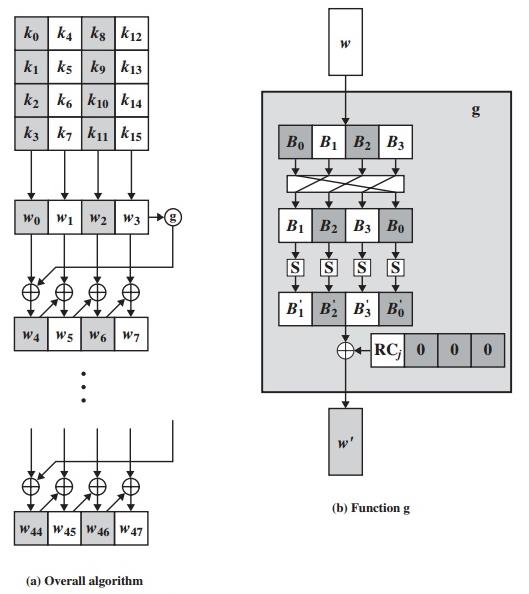
1.RotWord :
Performs a one-byte circular left shift on a word. This means that an input word [B0, B1, B2, B3] is transformed into [B1, B2, B3, B0].
2.SubWord :
Perform a byte substitution for each byte of the word returned by the previous step by using the same 16 × 16 lookup table as used in the SubBytes step of the encryption
rounds.
3.Rcon:
The result of steps 1 and 2 is XORed with a round constant, Rcon[j]. The round constant is a word whose three rightmost bytes are always zero. Therefore, XOR’ing
with the round constant amounts to XOR’ing with just its leftmost byte.
The round constant for the i th round is denoted Rcon[i]. Since, by specification, the three rightmost bytes of the round constant are zero, we can write it as shown below.
The left hand side of the equation below stands for the round constant to be used in the i th round. The right hand side of the equation says that the rightmost three bytes
of the round constant are zero.
Rcon[i] = (RC[i], 0x00, 0x00, 0x00)
The only non-zero byte in the round constants, RC[i], obeys the following recursion:
RC[1] = 0x01
RC[i] = 0x02 × RC[i − 1]
The values of Rcon[i] in hexadecimal are

The addition of the round constants is for the purpose of destroying any symmetries that may have been introduced by the other steps in the key expansion algorithm.
The key expansion algorithm ensures that AES has no weak keys. A weak key is a key that reduces the security of a cipher in a predictable manner.
The AES expansion key algorithm designed to be resistant to known cryptanalytic attacks. The inclusion of a round-dependent round constant eliminates the symmetry
or similarity, between the ways in which round keys are generated in different rounds.
This step consists of using a 16 × 16 lookup table to find a replacement byte for a given byte in the input state array. This is a byte-by-byte substitution using a rule
that stays the same in all encryption rounds.
Let xin be a byte of the state array for which we seek a substitute byte xout. We can
write xout = f(xin).
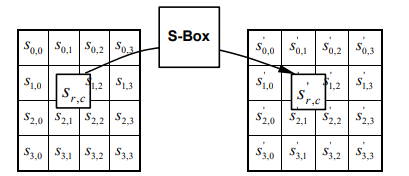
The goal of the substitution step is to reduce the correlation between the input bits and the output bits at the byte level. The bit scrambling part of the substitution step
ensures that the substitution cannot be described in the form of evaluating a simple mathematical function.
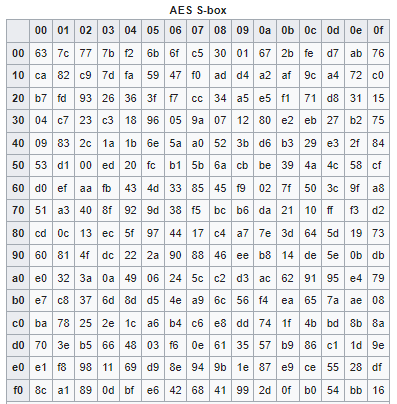
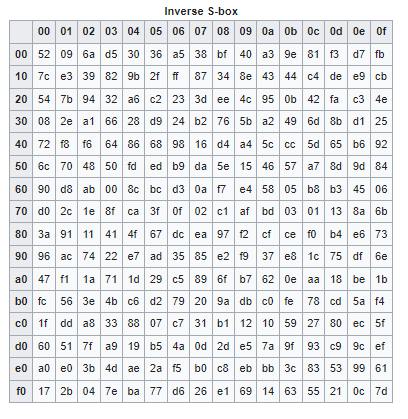
Similarly, during decryption, each value of state is replaced with the corresponding Inverse S-Box value.
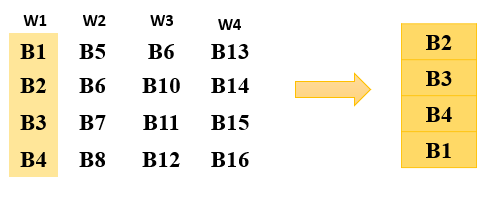
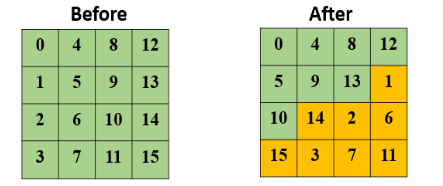
Shift Row :
During the shiftrow operation we perform circular shift of each row. The matrix is formed vertically but shifted horizontally.
The ShiftRows transformation consists of
(i) not shifting the first row of the state array at all
(ii) circularly shifting the second row by one byte to the left
(iii) circularly shifting the third row by two bytes to the left.
(iv) circularly shifting the last row by three bytes to the left.
For decryption, the corresponding step shifts the rows in exactly the opposite fashion. The first row is left unchanged, the second row is shifted to the right by one
byte, the third row to the right by two bytes, and the last row to the right by three bytes, all shifts being circular.
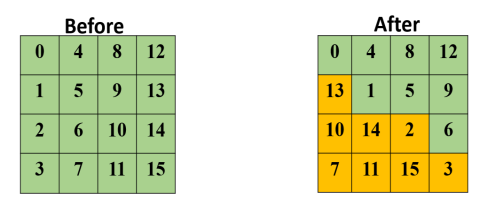
Mix Column:
Each byte in a column is replaced by two times that byte, plus three times the the next byte, plus the byte that comes next, plus the byte that follows.
[Note that by ‘two times’ and ‘three times’, we mean multiplications in GF(2 8 ) by
the bit patterns 000000010 and 00000011, respectively.] The predefined matrix is multiplied with the State matrix to form the matrix
multiplication and followed by the Galois field multiplication using the L Table and E Table.

The first result byte is calculated by multiplying 4 values of the state column against4 values of the first row of the matrix. The result of each multiplication is then
XORed to produce 1 Byte.
B1 = (B1 * 2) XOR (B2 * 3) XOR (B3 * 1) XOR (B4 * 1)
The second result byte is calculated by multiplying the same 4 values of the state column against 4 values of the second row of the matrix. The result of each
multiplication is then XORed to produce 1 Byte.
B2 = (B1 * 1) XOR (B2 * 2) XOR (B3 * 3) XOR (B4 * 1)
The third result byte is calculated by multiplying the same 4 values of the state column against 4 values of the third row of the matrix. The result of each
multiplication is then XORed to produce 1 Byte.
B3 = (B1 * 1) XOR (B2 * 1) XOR (B3 * 2) XOR (B4 * 3)
The fourth result byte is calculated by multiplying the same 4 values of the state column against 4 values of the fourth row of the matrix. The result of each
multiplication is then XORed to produce 1 Byte.
B4 = (B1 * 3) XOR (B2 * 1) XOR (B3 * 1) XOR (B4 * 2)
Similarly done for other columns also.
Gallois Field Multiplication:
The result of the multiplication is simply the result of a lookup of the L table, followed by the addition of the results, followed by a look up to the E table. The
addition is a regular mathematical addition represented by +, not a bitwise AND.
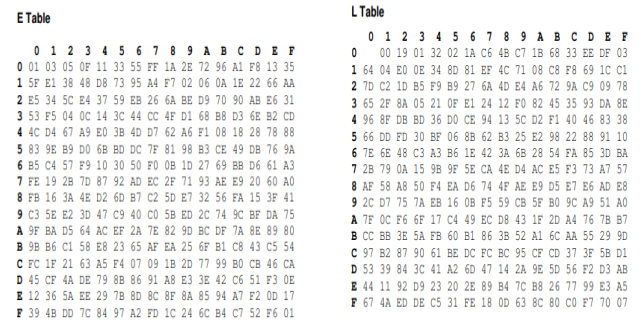
All numbers being multiplied using the Mix Column function converted to HEX will form a maximum of 2-digit Hex number. We use the first digit in the number on the
vertical index and the second number on the horizontal index. If the value being multiplied is composed of only one digit, we use 0 on the vertical index.
For example, if the two Hex values being multiplied are AF * 8 we first lookup L (AF) index which returns B7 and then lookup L (08) which returns 4B.
Once the L table lookup is complete, we can then simply add the numbers together.
The only trick being that if the addition result is greater than FF, we subtract FF from the addition result.
For example AF+B7= 166. Because 166 > FF, we perform: 166-FF which gives us 67.
The last step is to look up the addition result on the E table. Again, we take the first digit to look up the vertical index and the second digit to look up the horizontal
index.
For example, E (67) =F0
Therefore, the result of multiplying AF * 8 over a Galois Field is F0. During decryption: Similar steps are followed as stated above, the difference being
that we use a different predefined matrix so matrix multiplication.
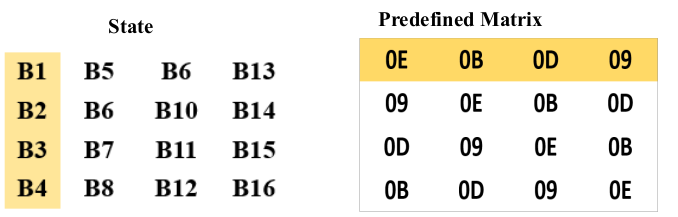
B1 = (B1 * 0E) XOR (B2 * 0B) XOR (B3 * 0D) XOR (B4 * 09)
B2 = (B1 * 09) XOR (B2 * 0E) XOR (B3 * 0E) XOR (B4 * 0D)
B3 = (B1 * 0D) XOR (B2 * 09) XOR (B3 * 0E) XOR (B4 * 0B)
B4 = (B1 * 0B) XOR (B2 * 0D) XOR (B3 * 09) XOR (B4 * 0E)
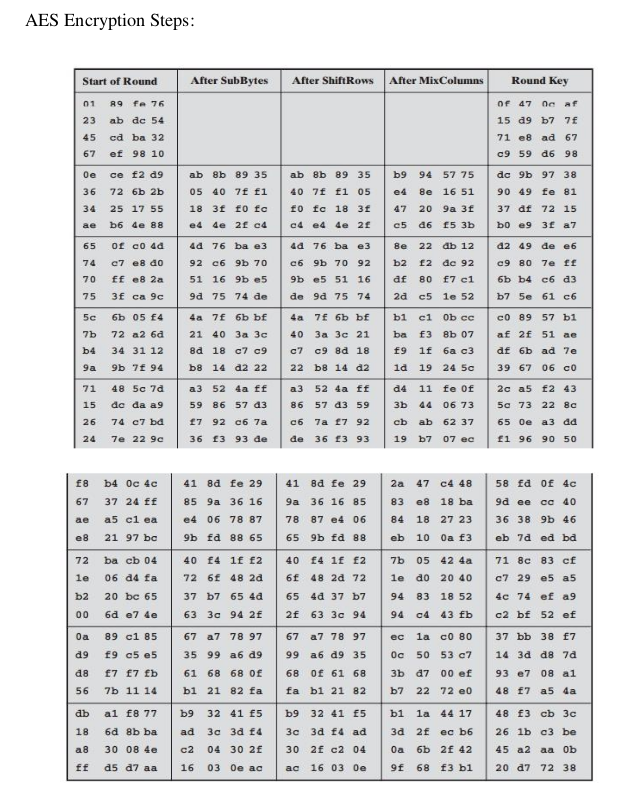
AES Encryption Example: –
One complete calculation of AES encryption for a specific message block is included in this section with results in each stage.
For this example, the plaintext, key, and resulting ciphertext are Plaintext: 0123456789abcdeffedcba9876543210
Key: 0f1571c947d9e8590cb7add6af7f6798
Ciphertext: ff0b844a0853bf7c6934ab4364148fb9
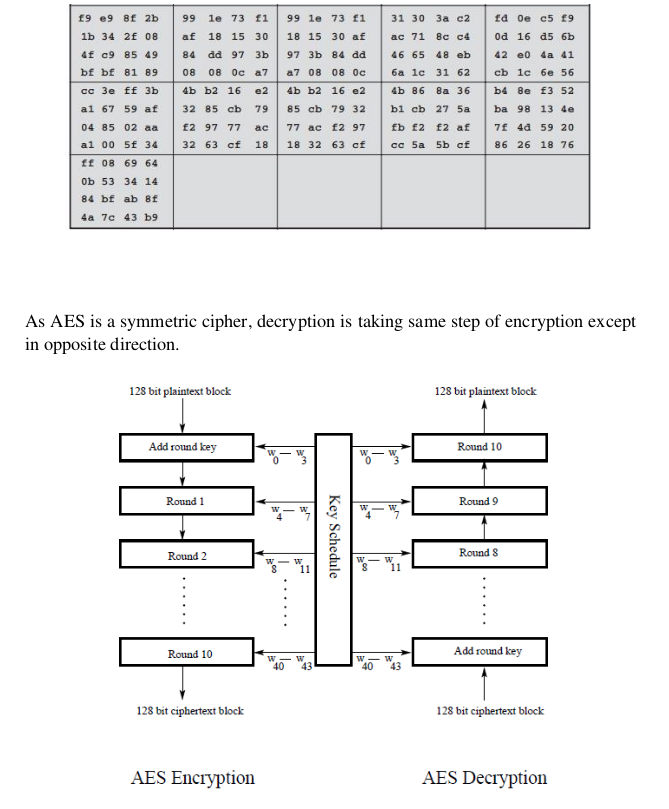
In the table below the left-hand column shows the four round-key words generated
for each round. The right-hand column shows the steps:
Key Expansion Steps:-

Algorithm Implementation
As part of this mini project, we have implemented the AES algorithm encryption and decryption as a C library for low end microcontrollers especially aiming the
TIVA C board having TM4C123GH6PM as the microcontroller. All three key lengths (16, 24 and 32 bytes) are supported in this library and the preferred key
length can be selected by changing the macro definition #define AES_BIT 128 in aes_fun.h file by appropriately changing to 128/192/256 for 16/24/32 Byte key
length.
While implementing the algorithm, we have tried to optimize the implementation in such a way that time taken by the algorithm execution is minimum. Few of the
optimization done are,
• Encryption/Decryption steps are combined wherever possible. For example, Substitution of bytes and shift row operation are done
together. Thus, time taken for function call, stacking and return are minimized.
• Wherever possible, loops are unrolled and written explicitly. This may increase the code size by little amount but the jump instruction and
condition calculation etc can be minimized and thus time can be optimized.
• Memory allocation of expanded key are done based on the
#define AES_BIT Macro thus unwanted memory allocation for lower key
length are avoided.
• Conditional compilation is used to handle the special case of the different key lengths rather than mixing all conditions and checking in
the code. This will help to reduce the code size and optimize for the specific key length selected.
• Use of computer architecture for optimum use of instructions.TM4C123GH6PM is a 32 bit microcontroller, thus shift row operations
are done using 32 bit operation so that 4 byte can be calculated same time.
Library provides two types of function to user. One is basic set of function which will work on one single block of message ie 16 bytes of message. Second set of
functions support longer message encryption and decryption based on standard block cipher modes such as ECB (Electronic Code Book) and CBC (Cipher BlockChaining). Basic functions can be used by user to implement other modes such as CFB(Cipher Feedback), PCBC(Propagating Cipher Block Chaining etc).
Basic Encryption Decryption functions
Basic encryption function supported by the library are explained in this section.
These basic functions are Key Expansion, and encryption decryption function for
single block of message.
1) void Key_Expansion( unsigned char* key)
This function receives starting address of initial bytes of key as input argument. Using this function will calculate rest bytes required depending upon the
AES_BIT Macro defined in aes_fun.h file and will store those bytes to memory location followed by the predefined key.
2) Void AES_Encrypt(unsigned char* Message, unsigned char* Result) This function receives the starting address of 16 byte message to be encrypted
and starting address to where the encrypted message to be stored. Function calculates the encrypted message by going through the required
steps and number of rounds based on the key length defined using the macro and once computed the result will be written to the starting address given in input
argument.
3) Void AES_Decrypt(unsigned char* Message, unsigned char* Result)
This function receives the starting address of 16 byte message to be decrypted and starting address to where the decrypted message to be stored.
Once the decryption is over the result will be written to the location starting from address given in input argument.
These three basic functions can be used by user for implementing AES encryption in TM4C123GH6PM without worrying about the AES algorithm or its internal way
of working.
C library provided by this mini project gives two files, aes_fun.h which is the header
file having declarations of these functions and aes_fun.c file which is having thedefinitions of these functions. Internal functions used to implement the algorithm etc
is also included in these files.
It is also possible for user to just change the macro and small piece of conditional compilation code so that a custom AES implementation with different number of
rounds etc can be implemented. User can experiment on that by changing appropriate portions in .c and .h files as per their requirement.
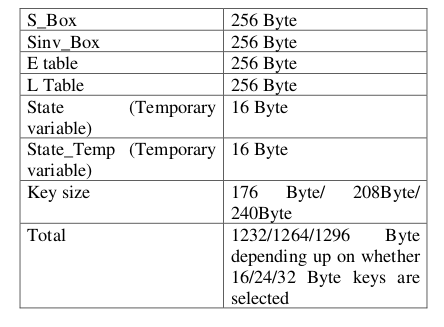
Memory requirement and timing details
S Box, Sinv_Box, E table and L table are saved as look up table in memory. Thus the AES library is having a minimum memory requirement. That is listed below.
Time Taken for Encryption and Decryption
Time taken for one block of message to be encrypted and decrypted using this implementation was measured using systick timer. Time taken with different
compiler optimization flags were measured and tabulated and given below.
All the below timings were calculated using 16MHz clock frequency. Thus timing should be recalculated proportionally when different clock frequency are used.
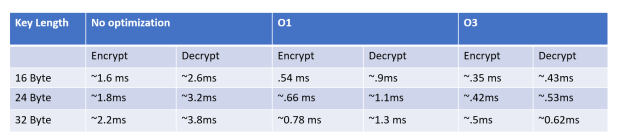
It is evident from the table that even without any compiler optimization, library functions can be directly used for low data rate applications where data is generated
in order of 8KSPS and all.
AES Encryption and Decryption for longer Messages Some time user may have to encrypt messages of longer length which may or may
not be of multiple of 16 bytes. In those cases, AES being a block cipher, we need to divide the message into different block and do encryption on each of that block.
There are some standard modes being used in block ciphers for encrypting long length messages based up on the way encryption decryption is done. Some of the
commonly used techniques are ECB(Electronic codebook), CBC(Cipher block chaining), CFB(Cipher feedback etc). Library supports ECB and CBC modes. If any
other modes to be implemented user can use basic encryption decryption function explained above to do the same.
Another thing to done while encrypting longer message is padding of message to multiple of 16 bytes if it is not. This is done automatically in these supported modes
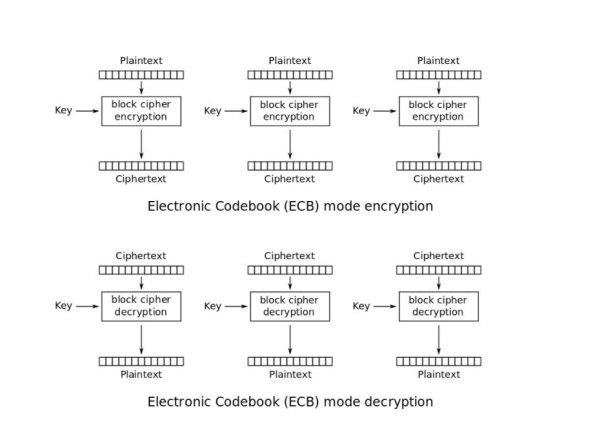
of ECB and CBC. Electronic codebook Encryption decryption.
Electronic codeblock is simplest technique where input message is divided into blocks and do the encryption one by one. Encryption can be even done in parallel as
there is no interdependency between the message that is encrypted.
• Void Encrypt_Message_ECB(char * Message, int Message_length, char* Result)
This function takes the starting address of message to encrypted along with message length and starting address where result to be stored as argument. Function will pad the message with 0x00 if message length is not multiple of 16 bytes and divide the message to blocks of 16 byte and do the encryption block by block.
• Void Decrypt_Message_ECB(char * Message, int Message_length, char* Result)
This function takes the starting address of message to decrypted along with message length and starting address where result to be stored as argument. As this is
decryption message length should be multiple of 16 anyway. Function will decrypt block by block and store the result to address given as argument.
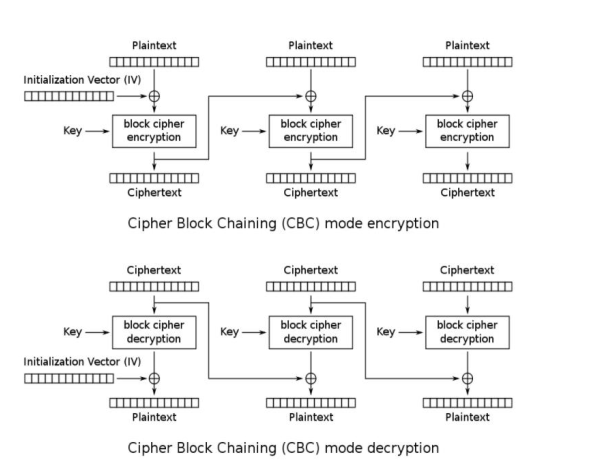
Cipher Block Chaining(CBC) Encryption decryption In CBC mode, each block of plain text is XORed with the previous ciphertext block
before being encrypted. This way, each ciphertext block depends on all plaintext blocks processed up to that point. To make each message unique, an initialization
vector must be used in the first block.
• Void Encrypt_Message_CBC(char * Message, int Message_length, char* Result)
This function takes the starting address of message to encrypted along with message length and starting address where result to be stored as argument. Function
will pad the message with 0x00 if message length is not multiple of 16 bytes and divide the message to blocks of 16 byte and do the encryption block by block.
• Void Decrypt_Message_CBC(char * Message, int Message_length, char* Result) This function takes the starting address of message to decrypted along with
message length and starting address where result to be stored as argument. As this is decryption message length should be multiple of 16 anyway. Function will decrypt
block by block and store the result to address given as argument. CBC mode allows better diffusion of message compared to ECB. But it requires additional 16 byte of initialization vector and will take up that space also.
IV can be changed in aes_fun.c.
Code Organization: –
Main.c :- This file contains the UART console program written for testing for AES encryption decryption. UART initialization, systick initialization,
command reception formatting etc are done in this file.
aes_fun.c :- This file contains the definitions of the AES related functionality.
aes_fun.h :- This file contains the declaration of function related to AES.
Testing and Results
To test the implementation in TIVA board, A UART console program was written where encryption and decryption of messages can be done through console
commands.
Commands included are given below with their format.
1) Encrypt STR/HEX message in string or hex format:- this command can be used to provide the message to be encrypted in string or Hex format. But
message length should be fixed to 16 byte in this case. Tiva Board will reply with encrypted message and time taken for encrypting this 16 byte this 16 byte
in terms of count taken by the systick counter. This count multiplied with 62.5ns will give absolute time taken.
2) Decrypt STR/HEX message in string or hex format:- this command can be used to provide the message to be decrypted in string or Hex format. But the
message length should be fixed to 16 byte in this case. Tiva Board will reply with decrypted message and time taken for decrypting this 16 byte in terms of
count taken by the systick counter. This count multiplied with 62.5ns will give absolute time taken.
3) Encrypt ECB message in string: – this command can be used to provide the message to be encrypted in ECB mode in string format. Message length can
be more than 16 characters in this case.
4) Decrypt ECB message in hex: – this command can be used to provide the message to be encrypted in ECB mode in hex format. Message length can be
more than 16 characters in this case.
5) Encrypt CBC message in string: – this command can be used to provide the message to be encrypted in CBC mode in string format. Message length can
be more than 16 characters in this case.
6) Decrypt CBC message in hex: – this command can be used to provide the message to be encrypted in CBC mode in hex format. Message length can be
more than 16 characters in this case. In order to verify the results obtained we used a online AES encryption decryption
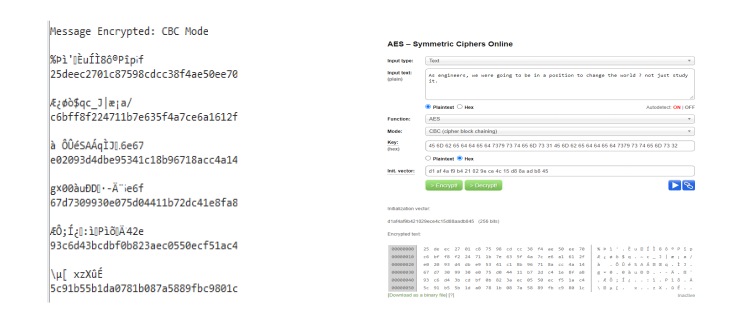
tool, http://aes.online-domain-tools.com/. Some of the results obtained is given below.
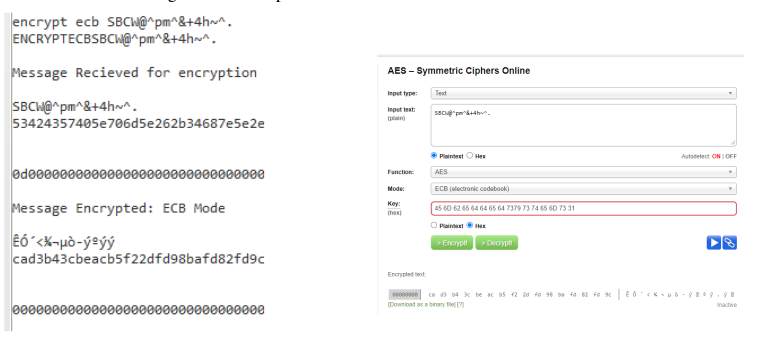
Result 1:- (Key length 16 byte)
• Key :- Embeddedsystems1
• Message : SBCW@^pm^&+4h~^.
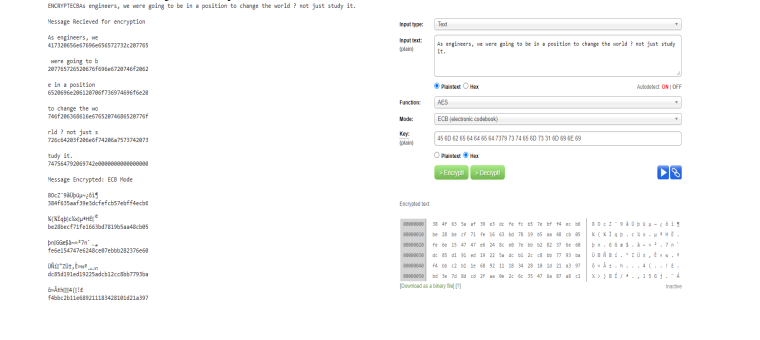
Result 2:- ECB Encryption (24 Byte)
• key = Embeddedsystems1miniproj
• message: As engineers, we were going to be in a position to change the world
? not just study it.
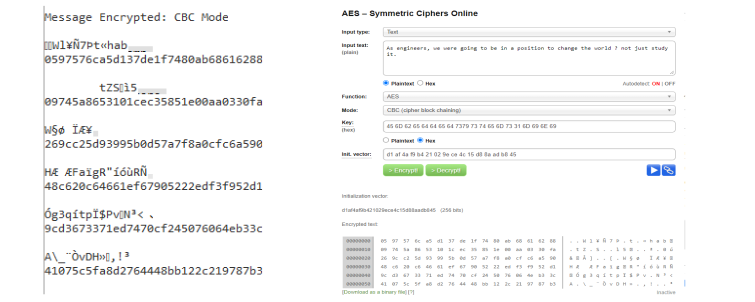
Result 3:- CBC Encryption (24 Byte) IV[]={0xd1, 0xaf, 0x4a, 0xf9, 0xb4, 0x21, 0x02,
0x9e, 0xce, 0x4c,
0x15, 0xd8, 0x8a, 0xad, 0xb8, 0x45 };
• key = Embeddedsystems1miniproj
• message: As engineers, we were going to be in a position to change the world
? not just study it.
Result 4:- CBC Encryption (32 Byte)
• key = Embeddedsystems1Embeddedsystems2
• message: As engineers, we were going to be in a position to change the world
? not just study it.
Conclusion:
AES encryption decryption algorithm is implemented using a c library from scratch.Simple optimization techniques like loop unrolling, combining the functions
wherever possible, minimal function call etc were tried while implementing the algorithm and to minimize the time taken for encryption and decryption.
Time taken for encryption and decryption were measured with different compiler optimization and it was found that the implementation is suitable for a moderate data
rate upto 10KSPS. Further optimization can be studied seeing the disassembly code and other techniques etc. Other modes of block cipher encryption technique like
CFB, PCBC also can be added to the library.
Recent Comments